07 marzo, 2017

Cuadrados Mágicos

Mundo matemático
Por Alberto Coto 0 Comentarios

Observemos la originalidad de este cuadrado de orden 4

Como ya hemos dicho, los cuadrados mágicos se utilizaron en toda clase de supersticiones, observa este cuadrado mágico de orden 6. Todas sus filas columnas y diagonales suman 666, es decir el número del diablo, por eso es conocido como Cuadrado Mágico Satánico.

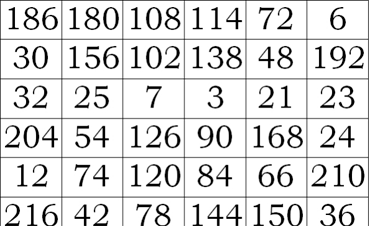
Ricemos el rizo de la fantasía y de la magia, porque el siguiente cuadrado mágico (creado por A.W. Johnson) no sólo es satánico, sino que además todos los números que lo integran son números primos.

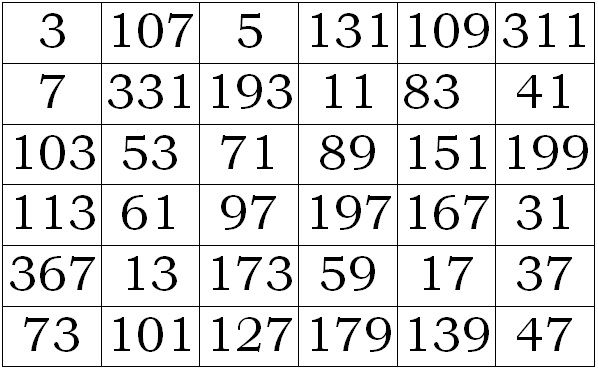
Nuestro siguiente cuadrado mágico, además de ser peculiar, tiene la particularidad de que fue creado, nada más y nada menos, que por Benjamin Franklin. Y es que el inventor del pararrayos era muy aficionado a estos mágicos pasatiempos.

Entre las propiedades del cuadrado mágico de Franklin podemos observar las siguientes:

2) Cada fila suma 260
3) Cada columna suma 260
4) La primera mitad de cualquier fila suma 130
5) La segunda mitad de cualquier fila suma 130
6) La primera mitad y la segunda mitad de cada columna suman 130
7) Los cuatro números de las esquinas más los cuatro números del centro suman 260
8) La suma de los cuatro números de cualquier cuadrado de 2 x 2 es 130
9) Los cuatro números de una diagonal que sube más los cuatro números de la diagonal respectiva que bajan suma 260.

Métodos de Resolución

1.- Cuadrados mágicos de orden impar: Método de Loubere

El primer método para la construcción de cuadrados mágicos de orden impar se debe a De La Loubere que fue embajador de Luis XIV en Siam los años 1687 y 1688, y publicó en 1691 «Du royaume de Siam», en el que dio a conocer su método de construcción de cuadrados impares. Veamos en qué consiste construyendo un cuadrado mágico de orden 5. Para comprender mejor el método vamos a llamar a cada celda por su fila y columna, es decir:

Nos imaginamos que nuestro cuadrado es un cilindro ‘imposible’, es decir, nos imaginamos que las filas 1 y 5 están unidas, así como las columnas 1 y 5. Y empezamos colocando primero el 1 en la posición central de la fila superior (1,3) y vamos rellenando en diagonal, es decir, el 2 se coloca en la posición (5,4) (fila 5, columna 4), el 3 en la posición (4,5), el 4 en la (3,1), y así sucesivamente. Cuando al intentar colocar un número en la posición que debe ocupar nos la encontramos ya ocupada colocamos ese número justo debajo del último que hemos colocado y continuamos colocando en diagonal. Veámoslo en varios pasos:

2.- Cuadrados mágicos de orden impar: Método de Bachet

Otro método para construir cuadrados mágicos de orden impar es el método de Bachet, diseñado por el matemático francés Claude-Gaspar Bachet de Méziriac (1581-1638), es un método muy visual y sencillo. Vamos a utilizarlo para construir un cuadrado mágico de orden 5.

Tenemos que crear el siguiente dibujo y distribuir los números de forma consecutiva y de esta forma:

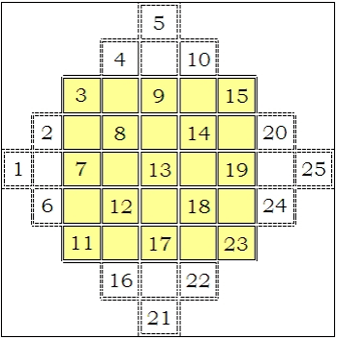
Los números que han quedado dentro del cuadrado de 5 por 5 los dejamos, y colocamos los números que han quedado fuera del cuadrado en las posiciones opuestas que quedaron libres. De esta forma nos quedará el siguiente cuadrado mágico de orden 5 (puedes comprobar que las sumas de filas, columnas y diagonales dan 65).

3.- Cuadrados mágicos de orden 4k

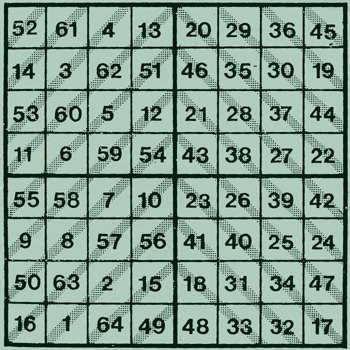
Vamos a construir un cuadrado mágico de orden 4k y lo rellenamos con los números del 1 al (4k)2 dispuestos de forma consecutiva (en nuestro ejemplo, el valor de k es 2, y los números serán, por lo tanto, del 1 al 64). A la vez dividimos el cuadrado grande en submatrices cuadradas de orden 4, tal como se muestra en la figura.

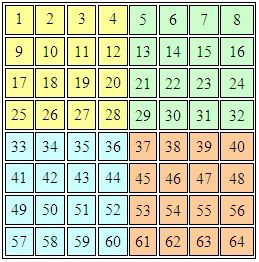
A continuación, tachamos cada submatriz con una X.

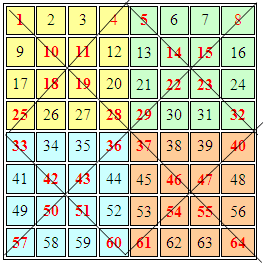
Los números que están situados en celdas por donde no pasan las X se mantienen en su lugar, y por los que sí pasa la X los vamos a intercambiar con su simétrico, invirtiendo de esta forma el orden en que han sido colocados en el cuadrado.

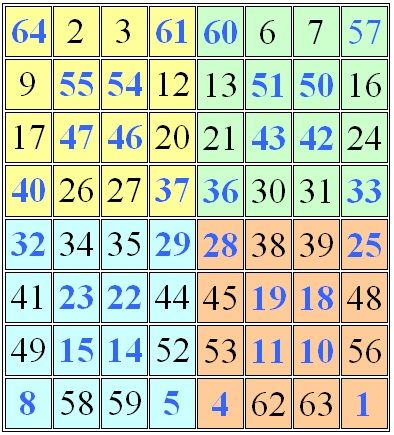
Y de esta forma, ya hemos construido un cuadrado mágico de orden 8, que a su vez tiene en su interior otros cuadrados mágicos de orden 4.

Fuente: “Fortalece tu mente”, Alberto Coto (editorial EDAF, 2007)